Rumus Segitiga Sebangun

21 Feb, 2021 Posting Komentar

Dua buah segitiga dikatakan sebagun jika memiliki bentuk yang sama tetapi ukurannya berbeda. Kesebangunan berkaitan dengan membandingkan 2 bangun datar.

Kesebangunan Pada Segitiga Idschool

Berdasarkan dari gambar bangun segitiga ABC dan segitiga PQR di atas diketahui bahwa A P sisi AC PR serta Q R.

Rumus segitiga sebangun. Sedangkan dua bangun datar dapat dikatakan kongruen apabila diantara kedua bangun datar tersebut. Kesebangunan merupakan salah satu bagian dari ilmu geometri. Untuk membuktikan bahwa kedua segitiga tersebut sebangun kita tidak perlu membandingkan semua panjang sisi dan besar sudut yang bersesuaian tetapi kita bisa membuktikannya dengan menggunakan salah satu saja syarat kesebangunan segitiga yang sudah dijelaskan di atas.

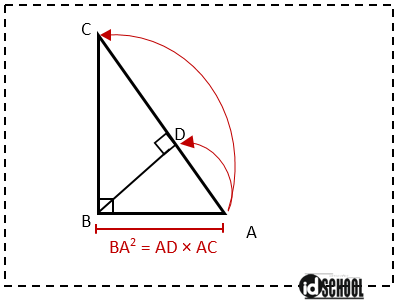
Ketiga segitiga ini adalah segitiga yang sebangun dan dengan memanfaatkan kesebangunan dari ketiga segitiga tersebut kita akan mendapatkan rumus untuk menentukan panjang AB AC dan AD. Rumus kesebangunan ini juga mendasari ilmu trigonometri. Dari kesebangunan segitiga-segitiga tersebut diperoleh beberapa.

Dua bangun datar dapat dikatakan sebangun apabila setiap sisi-sisi dari kedua bangun tersebut memiliki nilai perbandingan yang sama. Segitiga ABC yang lebih besar sebangun dengan segitiga kecil ADE sehingga perbandingan panjang sisi-sisi yang bersesuaian akan sama. Dua bangun yang sama persis memang disebut sebagai kongruen.

Dengan demikian sangat penting bagi kita untuk mengingat rumus kesebangunan ini. Dengan demikian DB AB AD 15 cm 10 cm 5 cm Dari soal berikut tentukan. Rumus tersebut diperoleh melalui persamaan perbandingan sisi pada dua buah segitiga yang sebangun.

Ini berarti salah satu perbandingan sisi bersesuaiannya adalah. Rumus Segitiga - Luas Keliling dan Contoh Soalnya Bangun segitiga ABC ini sebangun dengan bangun segitiga PQR yakni. Kedua segitiga tersebu masih terlihat sama bahkan ketika kedua segitiga tersebut di rotasi ataupun dicerminkan.

Segitiga yang kongruen merupakan segitiga yang memiliki bentuk dan ukuran yang sama. Itulah tadi cara mendapatkan rumus kesebangunan pada segitiga siku siku. Dalam menghitung salah satu sisi segitiga yang belum diketahui dari dua segitiga sebangun kita dapat menggunakan cara sebagai berikut.

Syarat dua segitiga sebangun adalah sisi-sisi yang bersesuaian sebanding atau sudut-sudut yang bersesuaian. Sudut-sudut yang bersesuaian yaitu sudut QPR dengan sudut QST sudut PQR dengan sudut SQT serta sudut QRP dengan sudut QTS. Dari dua gambar di atas untuk membuktikan bahwa gambar tersebut adalah sebangun mdapat kita lihat dengan menguraikan beberapa sifat sifatnya yaitu.

Menurut ilmuwan Matematika Euclid yg menemukan Bangun Datar Segi Tiga ini mengatakan bahwa jumlah ketiga sudut di suatu Segitiga pd bidang datar ialah sebesar 180 derajat. Kedua segitiga di atas. Pada gambar di atas terdapat dua bangun segitiga yaitusegitiga PQR dan segitiga QST.

Rumus Kesebangunan dan Contoh Soalnya. Diketahui DABC sebangun dengan DKLM. Oleh karena itu Rumus Matematika kali ini akan membahas mengenai segitiga kongruen agar temen-temen mudah memahami mana segitiga-segitiga yang termasuk dalam segitiga kongruen.

Kekongruenan Ketika kita memperhatikan lantai rumah kita terdapat ubin-ubin yang dipasang dilantai dengan bentuk dan ukuran yang sama. Maka akan didapat dua segitiga siku-siku yang baru yaitu segitiga siku-siku ABD siku-siku di D dan segitiga siku-siku ACD siku-siku di D. Karena segitiga PSR dan segitiga RSQ merupakan segitiga-segitiga yang sebangun maka perbandingan dari panjang sisi-sisi yang bersesuaian besarnya sama.

Untuk membandingkan sisisisi yang bersesuaian seletak perhatikan sisi di depan sudut yang berukuran sama. Rumuscoid Setelah sebelumnya kita membahas tentang rumus volume bola kali ini kita akan membahas materi tentang rumus luas segitiga sembarang kita akan jabarkan secara detail dan lengkap dari pengertian segitiga sembarang sifat sifat rumus dan contoh soal dari luas segitiga sembarang. Rumus-rumus kesebangunan sangat dibutuhkan dalam geometri baik bidang datar maupun bangun ruang.

Perhatikan ilustrasi dua buah segitiga sebangun di bawah ini. Dari gambar di atas perbandingan sisi yang bersesuaian pada segitiga ABC dan KLM yaitu. Untuk membuktikan kesebangunan kedua segitiga tersebut bandingkan sisi-sisi dan sudut-sudut yang bersesuaian.

Perhatikan gambar dibawah ini. Syarat dua bangun datar sebangun adalah jika setiap sisi dari 2 bangun datar tersebut memiliki nilai perbandingan yang sama. Posting pada Rumus Matematika SMP Ditag contoh soal kesebangunan dan kekongruenan beserta jawabannya contoh soal segitiga kongruen contoh soal segitiga sebangun pada segitiga dengan garis-garis sejajar kesebangunan trapesium materi kesebangunan dan kekongruenan segitiga pengertian kesebangunan dan kongruen segitiga kongruen sisi.

Perhatikan segitga ADB dan segitiga BDC. Temukan dulu panjang sisi AB ambil perbandingan alas dan tinggi dari kedua segitiga seperti berikut ini. Pada segitiga tersebut sisi DE yang sejajar dengan BC sehingga diperoleh dua buah segitiga yang sebangun yaitu DADE dan DABC.

Dua buah segitiga bisa sobat katakan sebangun jika ia memiliki apa yang disebut kesebangunan. Kesebangunan dan kekongruenan merupakan bagian dari ilmu geometri. Kedua segitiga tersebut sebangun sehingga sudut-sudut yang bersesuaian sama besar.

Selanjutnya coba buktikan bahwa segitiga PSR sebangun dengan segitiga PRQ dan segitiga RSQ sebangun dengan segitiga PRQ. Pada kesempatan kali ini materi yang akan disampaikan meliputi kesebangunan dan kekongruenan. Rumus Segitiga Pengertian Bangun Datar Segitiga adlh Bentuk suatu gambar yg memiliki tiga buah sisi berupa garis lurus dan tiga sudut.

A D A B D E B C 3 p 3 3 2 2 3 p 3 3 6 2 p 9 2 p 9 6 2 p 3 p 1 5. Namun secara formal dalam konteks bangun datar jika terdapat dua buah bangun datar bisa disebut kongruen apabila dapat memenuhi dua syarat yakni. Posting pada Rumus Matematika SMP Ditag contoh soal kesebangunan segitiga kesebangunan dua segitiga kesebangunan segitiga siku siku pengertian sebangun rumus kesebangunan segitiga rumus segitiga sebangun segitiga dengan garis-garis sejajar soal kesebangunan segitiga dan pembahasannya Navigasi pos.

Tempatku Berbagi Ilmu Pengetahuan